Day three working through Software Foundations with Coq. Since I like to rant, and I love Darkest Dungeon, ENTER THE DARKEST PROOF. (Please don’t sue me!)

I am trying to prove a helper proof to use to rewrite another helper proof to use to rewrite another proof for the commutativity of multiplication. You can’t make this stuff up.
I just need to prove this where S n is n + 1:
m * S n = m + m * n.
Should be simple…
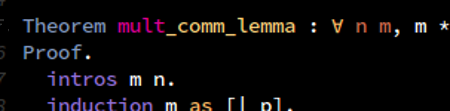
Theorem mult_comm_lemma : forall n m, m * S n = m + m * n.
Proof.
intros m n.
induction m as [| p].
Gives me:
2 subgoals, subgoal 1 (ID 291)
n * 1 = n + n * 0
subgoal 2 (ID 295) is:
n * S (S p) = n + n * S p
Wat.
I expected performing an induction on m to produce something like this:
2 subgoals, subgoal 1 (ID 291)
0 * S n = 0 + 0 * n
subgoal 2 (ID 294) is:
S p * S n = S p + S p * n
Instead it is inducting n?!

Wait.

No.
WHY?!
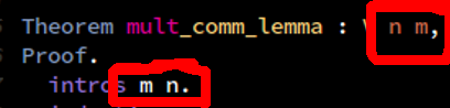
INTROS OVERWRITES THE NAMES IF PUT IN THE WRONG ORDER?!


